Cognitive Science 201A
Neuroanatomy and Neurophysiology
Name: _________________________
HOMEWORK #1:
Checklist:
(a) due by Wednesday 10/18/00, under my door (CSB 171)
(b) use this page as the first page
(c) staple all pages together
(d) one page maximum per answer (less than a page is better!)
(e) each answer on a separate page
(f) figures on same page as answer
(g) word-processor text with hand-drawn figures preferred
1. A cell has channels that only conduct a singly-charged
positive ion. Assume that these channels are opened momentarily
with the cell at rest (assume resting membrane potential is about
-70 mv). Indicate (a) which way the ions will flow (if at all),
and (b) how this will affect the membrane potential, for the
following three intracellular and extracellular concentrations of
this ion:
- inside: 120 mM outside: 120 mM
- inside: 36 mM outside: 7.4 mM
- inside: 41 mM outside: 1.3 mM
Then indicate (c) which way the ions will flow in the three
concentrations when the membrane potential is first clamped to
about -40 mv with a voltage clamp and the channels are then
momentarily opened.
2. Backpropagation is a technique for assigning error to
weights in one or more hidden layers. What exact feature of this
algorithm is hard to implement in real neural circuits? (be
specific--this means you have to briefly describe how backprop
works). Neurons in one part of the brain often project to another
part of the brain as a topographic map. How does this differ from
the networks typically used in cognitive models?
3. Ionic current flows at synapses made onto dendrites
generate electric potentials that take considerable time (milliseconds)
to propagate down to the cell body, despite the fact that changes
in intracellular potentials are conducted through cellular fluids
virtually instantaneously. Explain why this is by considering what
happens when a current step--a sudden and continuously maintained
increase in current--is injected into one location on a dendrite.
First draw a simple circuit diagram of a dendrite. Then qualitatively
describe the three different kinds of current flows (capacitive,
transmembrane resistive, longitudinal resistive) current flows in
the dendrite at three different points in time (before the current
went on, soon after the current went on, and a long time after the
current went on) and at two different spatial locations (near the
injection site, and far from the injection site). To reiterate,
this means you should mention a total of 18 things (3 currents x
3 times x 2 places).
4. Explain briefly how NMDA channels at a synapse detect
correlations between the activity in the pre- and post-synaptic
cells. In class we talked mainly about the involvement of NMDA
channels in LTP, which has often been studied in the hippocampus.
In the neocortex, in contrast to the hippocampus, the voltage-sensitive
current passing through NMDA channels contributes significantly to
post-synaptic potential. In light of this piece of information,
describe how, in the absence of LTP, the excitatory
voltage-sensitive NMDA current can allow a particular synapse to
have different effective synaptic weights at different times
(describe two different situations involving the same synapse)
5. (a) Why does the Linsker update equation contain only
pre-synaptic terms given that a Hebb rule is typically described
as changing the weight according to the correlation of pre- and
post-synaptic activity? (b) Give three examples of 5 pairs of
activation values for two units that illustrate positive, negative,
and zero correlation (c) Why do the weights from input units in
the center of the receptive field of a higher-layer unit increase
faster than weights in the periphery of the same receptive field
when there is a Gaussian 2-point correlation between input layer
units? (d) Explain how how Linsker learning rule can be thought of
as a matrix operating on a vector to yield another vector (say
explicitly what the input and output vectors are, and what the
matrix consists of).
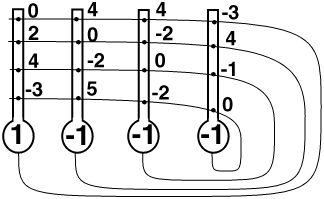
6. The diagram below shows a simple fully-connected Hopfield
network with 4 units (present state of each unit is shown inside
of it) and 12 weights (smaller numbers). Using the update and energy
equations given in class, determine: (a) what the present 'energy'
of the network is, (b) whether the network is now in a stable state,
and (c) what the energy will be after each unit in network has been
asynchronously updated once (left to right). This weight matrix is
not symmetric. (d) Very briefly, why is a symmetric weight (connection)
matrix required for the proof that no single unit update can ever
increase the energy?
7. In class, we considered a single-compartment integrate-and-fire
model described in Wilson and Bower (1989). (a) What are the
processes in real neurons are that are summarized by the alpha
function (conductance function for one channel type)? (b) Draw the
equivalent electrical circuit for a single neuron with one sodium
and one chloride channel attached to it. (c) Assume that an excitatory
synaptic input to a neuron is activated just before a GABA-A input
to the same neuron. Would the GABA-A channel conduct more, the
same, or less current than in the situation where it is activated
by itself? Explain your answer by giving a qualitative discussion
of the relevant equation. (d) Since a convolution is used to sum
up the effect of inputs at one connection, linear superposition of
conductances is assumed. Describe a situation (there are many
possibilities!) in a real neuron where linear superposition at a
connection would not hold.
8. Make diagrams of the normal connections of the two retinas
with the two dorsal lateral geniculate nuclei in the cat and an
Old World primate (N.B.: the dLGN's of cats and primates are
different!). Diagram how are these connections are changed in the
mutant Belgian sheepdog (the non-mutant sheepdog has a cat-like
dLGN). What does this mutant seem to imply about mechanisms thought
to be involved in stabilization of connections in the developing
nervous system (e.g., correlated activity, map- position-dependent
biochemical markers)? Give an example from the readings that comes
to the opposite conclusion.
