Continuous Processing with Symbolic Memory Representations

Continuous Processing with Symbolic Memory Representations:
An Activation Imagery Theory

James A. Levin

Laboratory of Comparative Human Cognition
University of California, San Diego

13 August 1981

A specter is haunting cognitive process models. The evidence for continuous cognitive processes has become ever stronger. This evidence is particularly convincing in the area of spatial information processing, demonstrating that mental spatial transformations traverse the intermediate states of orientation, size, and location (Cooper, 1975; Cooper & Shepard, 1973; Kosslyn, 1975; Robins & Shepard, 1977; Shepard & Judd, I976; Shepard & Metzler, 1971). This evidence for continuous change poses a serious challenge for the existing models of spatial information processing, both the various "symbolic" spatial models and even the attempts to develop low level "analog" models.

For example, let us examine a simple minded model for the mental rotation of letters represented in a semantic network (Levin, 1973). In this representation, the spatial structure of a letter is specified by a network of proximity relations between subparts of lines. For example, the structure of the letter P is given in Figure 1.

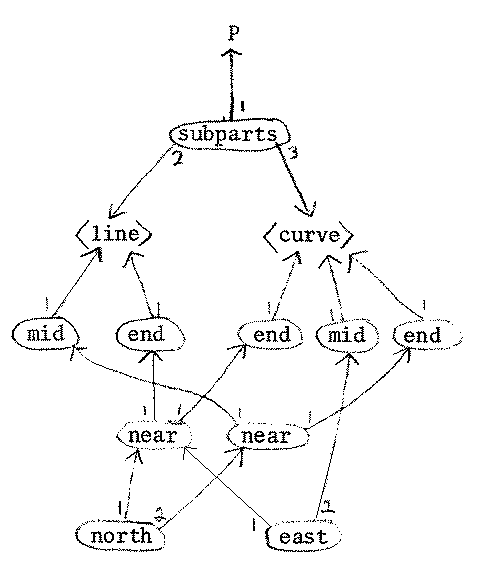
Figure 1: Representation of the letter "P"

With these building blocks, we can represent all of the letters of the alphabet (for example, see Levin, 1973, appendix 1). Most of this defining structure is orientation-free. To specify a normal upright orientation, two orientation relationships are used (in the above example, the relative orientation concepts of NORTH and EAST)! These orientation concepts are themselves further defined in memory, at least partially by the structure given in Figure 2.

Figure 2: Representation of interrelations between orientations

A Straw man "Symbolic" Model for mental rotation. A process model for mental rotation can now be defined. The model rotates the representation of the letter P clockwise by replacing each of the orientation relationships by the orientation in the clockwise direction (as specified by the relation "clockwise", as shown in figure 2). So, the first step in rotating the letter P would consist of replacing the EAST relationship by SOUTH, and the NORTH relationship by EAST. This stepwise rotation could continue as long as clockwise rotation was desired or until a specified new orientation was obtained.

The general predictions of this model fit the general data for mental rotation: larger rotations take longer. However, the rotation in this model proceeds in discontinuous jumps, while the data supports "continuous" rotation. The mathematical definition of continuity of a line is that for any two points on the line, there is an intermediate point. Empirically, data has been gathered that the internal representation for the orientation of the object at a time between two orientations is at an intermediate orientation (Cooper & Shepard, 1973; Cooper, 1975; Robins & Shepard, 1977).

These data have been widely taken to support "analog" models of mental imagery. And they certainly challenge the simple minded symbolic model of mental rotation presented above. But note that the evidence is for continuously changing processes, not continuous representations. To get a feeling for this distinction, let us examine one of the few explicit "analog" models of the spatial transformation of mental images, that of Kosslyn and Shwartz (1977). In their model, a mental image is represented by an array of cells (presumably an analog of the array of neural cells in the retina). Each cell in this image array has a brightness value, and the image of an object consists of a pattern of such cells. This kind of representation is "analog" in the sense that there is a direct mapping between each cell in the array and points of the object being represented.

In this "analog" model, continuous transformations (rotation, translation, scaling) can be performed by continuously mapping the contents of each cell into some other cell. In the particular computer implementation, this transformation was non-continuous (step-wise) but this is just a limitation of the modeling medium.

Or is it? This analog model scores points for being able to demonstrate continuous change. Yet, it doesn't answer the next question of why such changes are continuous in people. That is, the model is capable of continuous changes, but it is just as capable of non-continuous change. The restriction of non-continuous change is just tacked on. In fact, in the particular implementation, changes were done in large steps "to save time" (Kosslyn & Shwartz, 1977, p. 288). Why don't human spatial transformation processes also "save time" by performing a mental rotation or translation in one step, changing the representation of an object at one orientation or location immediately into a representation at another? Beyond demonstrating the capability for continuous transformation, a model of these processes should demonstrate the limitation that requires continuous change.

The next section will introduce a model of mental rotation which uses "propositional representations" that has both the capability for continuous spatial transformation and a limitation that explains continuous change in these tasks.

The Proteus Processing Framework

One way to deal with the evidence for continuous processing would be just to add more and more intermediate states of an essentially discontinuous process, until there was no way to distinguish tiny discontinuities from continuity. This is ugly. Another approach is to take this evidence (and other related evidence) for continuous processing seriously. Conventional process frameworks usually used for building cognitive process models are biased toward serial, discontinuous change. So we need to consider alternative processing frameworks that allow continuous processing.

One such framework, called Proteus (Levin, 1976), is derived from the "spreading activation" processing notions (Quillian, 1968; Collins & Quillian, 1972), augmented with a constraint satisfaction mechanism. There are a set of activations, each of which has a "salience" (a positive real number) that represents the current power of that concept. This salience dynamically changes, and if it drops below a certain level, the activation disappears. The salience of an activation is the result of the impact of other activations, and determines the impact that the activation has on the activations it influences.

Where do activations come from? An activation can be generated either through the action of pre-existing activations, or though the impact of something outside the scope of the cognitive process being modeled. The "outside" may be lower level perceptual or motor levels and/or higher level planning and goal pursuit levels.

Representing a continuum with "landmarks". Within "structural" models, continua have always been problematic. Some have approximated a continuum by a series of discrete classes of values, each interrelated by sequencing relations (Rumelhart & Levin, 1975, for instance). Others have just inserted a straight- forward real number into their representations (Palmer, 1975, for instance). Each of these proposals finds support in some areas and not in others. That is, we want a representation and a way of processing that is continuous in some ways and discrete in others. This can be achieved by a representation that is discrete but a processing framework that operates on it that can be continuous. Let us represent a continuum by a set of "landmark concepts", that represent prototypical values along the dimension. For instance, the dimension of orientation can be represented as shown in Figure 2.

In this case, we have four landmark orientations, in this case called North (up), East (right), South (down), and West (left). This representation is very similar to those previously criticized because of their "discrete" character. In fact, this representation is exactly the one used in the "straw man symbolic model" described previously. How do we obtain continuous change from such a discrete representation? Let us consider how we would represent in the Proteus framework the current state of being aware of the relative orientation two objects, say a star above a dot. We can have activations for the two object concepts:, both associated with activation for North. How can we now represent the same two objects, this time with the star to the right of the dot? Again, we can have activations for the objects, interrelated by an activation of East.

How about some intermediate orientation? To represent the awareness of the star both above and to the right of the dot, we can have activations for the two objects, interrelated by activations for both North and East. That is, we have multiple simultaneous activations of landmarks on a dimension to represent values in between those landmarks.

But these two activations just define the set of intermediate values - how do we represent the current awareness of a particular intermediate value? Remember that each activation has a current "salience" value, a positive real number that represents its current power. To represent the halfway intermediate point, we can have activations for the two landmarks that had equal saliencies; to represent values closer to one landmark, we can have the two activations, with the closer one more salient than the other. So the exact intermediate value is defined by the relative saliencies of the simultaneously active multiple landmark activations. We now have a way of representing any value on the continuum between the landmarks. In fact we have a natural way to represent continuous change from one landmark value to another, as shown by the "activation time line diagram" shown in figure 3. This shows graphically the continuous decrease in the salience of one landmark orientation and increase in the next, capturing the continuous change in orientation.

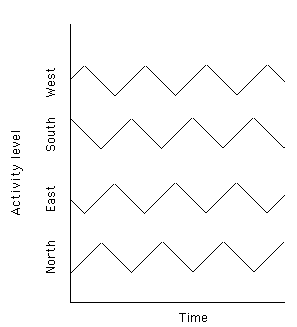
Figure 3: Activity graph showing the activity level of the four orientation landmarks during clockwise rotation.

What advantage is there to this representation over a single real numbered value for orientation? First, Rosch and Mervis (1975) have shown that there are "prototype" orientations, with special properties that distinguish them from other orientations. Not surprisingly, these special orientations are up, down, left, and right, the four landmark orientations shown in figure 2.

Secondly, there is a clear connection between the representation of orientation and actions that might be directed by such a representation. For example, the arm (as elsewhere in the human body) is controlled by sets of opposing muscle groups. Suppose we wanted to build a model of a person moving her arm in a circle with her eyes closed. A simple-minded model could contain an internal representation of a rotating arm, similar to the one described above, with interconnection between the salience of the landmark orientations and the muscle groups moving the arm, so that as a landmark became salient, it would activate the appropriate muscle groups. Going from opposing pairs of landmark orientations to the activation of opposing pairs of muscles is much easier than going from a single real number to the operation of those same actions.

Thirdly, this landmark representation of a continuum gives us a natural way to represent "fuzziness" or lack of precision in our knowledge. For example, certain knowledge that one object is directly East (right) of another can be represented by the activation of the concept East associated with activations of the two objects. Less precise knowledge of the same sort can be represented dynamically by activations for multiple orientation landmarks. Fairly certain knowledge of this fact can be captured by a highly salient activation of East and less salient activations for North and South. Highly uncertain knowledge can be represented by equally salient activations for North, East, and South. Obviously, any intermediate amount of precision can be represented by intermediate relative salience values. Thus we can represent by this landmark continuum scheme the uncertainty aspects which previously have been represented by "fuzzy sets" (Zadah, 1965) or by "fuzz boxes" (McDermott, 1980). The way proposed here provides not only a dynamic representation of uncertainly, but also the processing mechanism for using uncertain knowledge.

The limitation on continuous change. So far we have shown the capability for representing continuous change with this scheme. What about the limitation on continuous change? Why is there an upper limit on the rate of rotation? Why is there a relatively slow maximum rate of rotation (approximately 60 degrees per second for the rotation of three dimensional objects (Shepard and Metzler, 1971)). To put it more concretely, why cannot the salience of the landmark orientation be changed at whatever rate the external driving force operates? Note that this issue is not unique to the representation proposed here, but is a general problem for the other attempts to deal with continuous cognitive transformations. The representations in "analog" models do not have the property of "inertia".

Surprisingly enough, an interacting set of activations do have as a global property "mental inertia''. When mutual interactions exist, changes in the salience level of one activation do not occur instantaneously, but instead the change "reverberates" through the whole set, approaching a new level asymptotically. Even for sets of activations that interact solely through excitation and inhibition (Levin, 1976), changes on a mutually interacting set of activations have a "capacitive charge" effect on those activations (increases or decreases in the salience of the impacted activation follows an exponentially increasing or decreasing function). This "Gestalt" system property of a set of interacting concepts has previously been assumed as a primitive property of single elements (cf. McClelland, 1979). We can see it instead as a derived property of the overall system.

Multi-level representations of objects. Let us now go through a particular example of how to represent and then rotate some object. To simplify matters, let us start with a simple two-dimensional object, the letter P. Figure 2 shows a simple representation for this letter. The letter has a global orientation (upright, tilted, etc.) relative to some larger frame (the word it is in, or the sentence, or the page, etc.). The components of the letter also have orientations relative to each other. But there is a fixed relation between this "whole" orientation and the subpart orientations. The orientation of P specifies a relationship between the subparts of P in reference to the global framework. The orientation of a subpart defines the relationship between its subparts in reference to the more global object, in this case the letter P.

Relationships. The operation of the orientation concepts to maintain the consistency between the orientation of an object and the orientations of its subparts is a specific example of a general processing mechanism called here "relationships". A relationship is not really a new representational entity but instead is a new way to view the processing of the existing kinds of schema-like entities proposed to represent knowledge. Schemata package up knowledge into chunks, with a set of parameters forming the interface to the outside world. But most of these representational systems propose no processing framework. When simulation programs are written using these frameworks, they use standard control structures, often in relatively ad hoc ways. Thus, comparative evaluations of different representation systems are hindered by the ad hoc processing used to produce predictions of behavior.

Relationships embody a particular processing framework, which extends the relatively amorphous undisciplined spreading activation scheme. When a relationship is activated, it operates to enforce the ideal pattern constituting its definition (stored in long term memory) on the set of current activations. Each relationship that is active is simultaneously operating to change its parameters so that they are closer to the "ideal" for that relationship. Even though each is attempting to maintain local order, the changes made are global. This is the way that relationships "communicate" with each other: directly through global changes on shared parameters (or less directly though longer chains of global changes).

While each relationship tries to modify its parameters to be in the ideal relation that constitutes its definition, there may be resistance to its efforts, as other relationships may be simultaneously modifying the same activations in other directions. A relationship has an impact on its parameters to an extent directly proportional to its own salience. "Stronger" (more salient) relationship will thus have a bigger impact on their parameters, even if opposed by weaker relationships. It is through this global "pushing and shoving" that information gets integrated, with consistent information being cumulated through consistent effects on parameters, and contradictory information being reconciled through cancellation of conflicting effects.

Planar Rotation. Let us now look at an example of how relationships interact as components of a particular cognitive-process, mental planar rotation of an image. We have already seen how the results of such a process are expressed within this activation framework, as a continuous change in relative saliencies of activations of landmark orientation concepts. How can such a continuous change be orchestrated? Let us initially represent the concept for clockwise rotation, PLANAR-ROTATE-CL, as shown in figure 4.

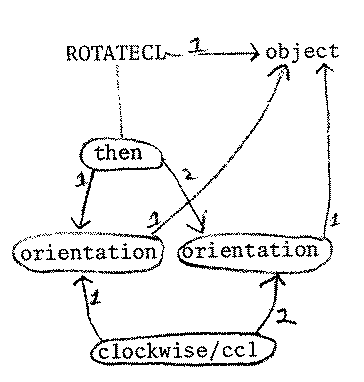
Figure 4: Representation of PLANAR-ROTATE-CL

This process is represented as the interaction of two component processes, the CLOCKWISE relationship and the temporal sequencing THEN relationship. The CLOCKWISE relationship activates the landmark orientation (specified in memory, as shown in figure 2), and the THEN concept associates with this concept a later time landmark (an "expectation" of the upcoming orientation). As time passes, this expectation may be met, and thus become the new current orientation for the next part of the rotation process. This dynamic change in activations can continue indefinitely, until the ROTATECL process ceases to be active.

This rotation process can be applied to an object, and the effects will propagate down through the subparts of the object. Because of the time course of this propagation, there will be a maximum rate of rotation, beyond which the image will distort in "paradoxical" ways, since the orientation of the whole will be "ahead" and therefore inconsistent with the orientation of the lagging subparts. Beyond this distortion phase, there will be a "blurred" phase, where the rotation process is operating so quickly that all orientations of the object are active at each time, a sort of "airplane propeller" effect. These stages (rigid rotation, distorted rotation, and blur) are described by Shepard and Judd (1978) in their studies of apparent rotation.

The rotation process is thus represented as a concept, separate from the concepts representing its effects (though, of course, related to those concepts). One advantage of this kind of multi-level representation is that certain otherwise mysterious visual illusions can now be understood. There are a family of motion aftereffect illusions that seem quite paradoxical. In the waterfall illusion and the spiral after-effect (Holland, 1965), we see movement without change of position. In the spiral aftereffect illusion, we see expansion or contraction without change of size. After we view a spinning spoked wheel, we see rotation without change of orientation. These all imply that the process is separately represented from the change that it creates, a multi-level representation like the one described here. In this framework, these illusions are simply represented by the activation of the process (of motion, expansion/contraction, rotation) with a conflicting activation of unchanging object attributes (location, size, orientation). The activation of the process, in aftereffects, can be through fatigue of the associated opposing process, while the activation of the unchanging object attributes can be through perception.

Three-dimensional rotation. So far we have restricted our attention to two-dimensional planar rotation. But people can mentally rotate images in three dimensions as well as in two (Shepard & Metzler, 1971; Pinker, 1980). Can the rotation model presented here be extended to the third dimension? Before we tackle the full complexities of three-dimensional rotation, let us decompose the process into simpler subprocesses.

When an object rotates in three dimensions, usually there is a mixture of pure planar rotation (rotation in the viewer's visual plane) and rotation out of the visual plane. In some cases, there is no planar component. How can we characterize these cases of pure out-of-plane rotation?

Pure out-of-visual-plane rotation. The dominant characteristic of out-of-plane rotation is the apparent change in the length of the object perpendicular to the axis of rotation. As objects rotate, the perpendicular lengths appear to shorten (as the object turns edge on) and then lengthen (as the object turns into our visual plane). For relatively flat objects, the lengths can shorten to almost zero, then lengthen to the maximum linear dimension of the object. A playing card can almost disappear as it turns edge on, and then continue to rotate full face on to us.

The change of perpendicular length follows a simple rule: for an object's perpendicular length L at an angle A out of the visual plane, the apparent (retinal) length is proportional to the product of L and the cosine of A. Although this rule has been known for centuries, it has remained unclear how to apply it within a model of visual processing. Let us construct a relationship, called SHAPE/ANGLE, that operates on its three parameters (object's perpendicular length, object's angle out of the visual plane, and apparent retinal length) according to this law of visual perspective. Given particular values for any two of these parameters, the SHAPE/ANGLE relationship operates to establish a particular value for the third. If a change occurs in any of the parameters, SHAPE/ANGLE operates to modify the others.

For example, suppose we have evidence for an object's perpendicular length and for its angle out of the visual plane. Then the SHAPE/ANGLE relationship will operate to produce an expectation of its apparent retinal length. Thus to mentally rotate an object directly out of the visual plan, all that is necessary is an process analogous to the planar rotation process described previously that operates on angle out of the visual plane (rather than orientation within the visual plane). The SHAPE/ANGLE relationship will then operate on the changed angle parameter (and knowledge of fixed object lengths) to produce the appropriate changes in retinal lengths.

As this relationship is defined in terms of the cosine function, what is the significance of the parts of that function that take on negative values? What is the interpretation of negative apparent lengths? Note that these negative retinal lengths are produced by this relationship for those positions of an object for which the lengths are obscured from view by the other side of the object. Thus a natural interpretation for these negative values is that these are lengths that exist but currently hidden from view.

The SHAPE/ANGLE relationship doesn't specify a one-to-one mapping among the parameters. Any given pair of values for an object's perpendicular length and retinal length map into two possible angles out of the plane, and both of these would be supported by the SHAPE/ANGLE relationship, in conflict with each other. This conflict is resolved on the basis of further information, for example, by the effect of the immediately previous orientation, for continuous rotation. In some cases people do in fact mistake an object rotating toward them for the same object rotating away (or vice versa). But usually we have other cues that disambiguate, such as the perceived size of the parts of the object.

The second aspect of rotation out of the visual plane is the change of size of parts of the object, as they get nearer and further from the viewer. Again, the perspective law for this change is well known: for a retinal size A (in visual degrees) and the object's linear extent L and distance D, the object's linear extent L is the product of the distance D and the sine of the retinal size A. This effect can again be represented by a relationship, which we will call SIZE/DISTANCE. Again, this is has three parameters, and acts to modify the actual value of each parameter so that it is in this specified "ideal" relation to the other two.

This SIZE/DISTANCE relationship is usually a secondary factor in rotation out of the visual plane, as it is seriously attenuated by distance, while SHAPE/ANGLE is less affected. The Frisbee spun in your hand undergoes much the same changes in retinal perpendicular distances as the rings of Saturn, but the size changes beyond a few meters of parts of ordinary objects quickly becomes unnoticeable. However, even a small effect may often be enough to disambiguate potential confusion, and SIZE/DISTANCE can cause major effects for nearby large objects rotating out of the visual plane.

Complex three-dimensional rotation. Now we have all the parts necessary to model complex mental rotation. Any given spatial rotation can be expressed as a composite of rotation in the visual plane and rotation out of the visual plane. Rotation is modeled in this framework by the simultaneous operation of relationships for planar rotation and for out-of-plane rotation. The operation of the planar rotation relationship produces a sequence of changes in the orientation of the object (and thus changes in the relative planar orientation of subparts). The operation of the out-of-plane rotation relationship produces two sets of changes: 1) changes in the apparent retinal lengths of the object perpendicular to the visual plane, and 2) changes in the retinal sizes of subparts that become closer or further from the viewer. It is through the global side-effects that each relationship has on its - parameters that the joint operation of these processes is coordinated, with consistent actions combining and conflicting actions canceling.

These relationships serve as the interface between object properties and modality specific properties. For example, SIZE/DISTANCE ties together the visual mode property of retinal size with the modality independent object property of size. Recent experiments on mental rotation in three-dimensions (Pinker, 1980) indicate that both the modality specific two-dimensional distances and modality independent three dimensional distances play a role in mental rotation. It is difficult to see how both these kinds of information can be integrated in so-called "analog" models of mental rotation. Within the activation framework proposed here, we represent three-dimensional rotation and its effects by providing a processing mechanism for the laws of perspective, tying together the modality independent and modality dependent information.

Imagery and perception. Much of the current theory concerning mental imagery points to the close ties to visual perception {Shepard & Podgorny, 1978; Palmer, 1978). Yet most of the current modeling has focused instead on the ties between mental imagery and memory (Kosslyn, 1975). The model of mental imagery presented here has direct ties to perception. In fact, the same relationships proposed for mental rotation can be seen as peculiar uses of mechanisms primarily used for visual perception, the mechanisms involved in maintaining object constancy.

Why would people be able to perform mental imagery? Surely it is not so that they can ask whether Volkswagens have fins. Instead these are the processes that are used in everyday life to move around in the world, identifying objects and maintaining constancy while we and the objects we perceive move about in the world. The SIZE/DISTANCE relationship is a mechanism for maintaining size constancy, so that as we move toward an object, it doesn't seem to grow. The planar rotation relationship help us see an object that we move past as stationary, rather than as rotating away from us. The SHAPE/ANGLE relationship helps us to see rigid objects instead of wildly distorting ones as we walk across a room.

Each of these relationships allow us to integrate whatever information we have about object from different percepts, from various modalities, from past experience, and from higher knowledge, to produce expectations of the immediate future. As long as these expectations are met, the object related knowledge of size, shape, orientation will remain unchanging, even though both we as observers are moving relative to the objects such that the retinal information is constantly changing. (If the expectations are violated, then we will see mysterious distortions in the world.)

Through the simultaneous interaction of many relationships we get complex cognitive processing. This same processing framework can be extended to other domains, like problem solving (Hutchins & Levin, l981) as well. Although each relationship is defined relatively simply, their interaction through global side effects produces the complex action characteristic of human cognitive processing.

References
Collins, A. M., & Quillian, M. R. How to make a language user. In E. Tulving & W. Donaldson (Eds.), Organization of memory. New York: Academic Press, 1972.

Cooper, L. A. Mental transformation of random two-dimensional shapes. Cognitive Psychology, 1975, 7, 20-43.

Cooper, L. A., & Shepard, R. N. Chronometric studies of the rotation of mental images. In W. G. Chase (Ed.), Visual information processing. New York: Academic Press, 1973.

Holland, H. C. The spiral after-effect. New York: Pergamon Press, 1965.

Kosslyn, S. M. Information representation in visual images. Cognitive Psychology, 1975, 7, 341-370.

Kosslyn, S. M., & Shwartz, S. P. A simulation of visual imagery. Cognitive Science, 1977, 1, 265-295.

Levin, J. A. Proteus: An activation framework for cognitive process models. Unpublished doctorial dissertation. La Jolla, CA: Department of Psychology, University of California, San Diego, 1976.

Levin, J. A. Network representation and rotation of letters. Unpublished manuscript. La Jolla, CA: Department of Psychology, University of

McClelland, J. L. On the time relations of mental processes: An examination of systems of processes in cascade. Psychological Review, 1979, 86, 287-330.

McDermott, D. A metric model of spatial processing. Paper presented at the Second Annual Conference on Cognitive Science, Yale University, June 1980.

Palmer, S. E. Fundamental aspects of cognitive representation. In E. H. Rosch, & B. B. Lloyd (Eds.), Cognition and categorization. Hillsdale, NJ: Erlbaum, 1978.

Palmer, S. E. Visual perception and world knowledge: Notes on a model of sensory-cognitive interaction. In D. A. Norman & D. E. Rumelhart (Eds.), Explorations in cognition. San Francisco: W. H. Freeman, 1975.

Pinker, S. Mental imagery and the third dimension. Journal of Experimental Psychology: General, 1980, 3, 354-371.

Quillian, M. R. Semantic memory. In M. Minsky (Ed.), Semantic information processing. Cambridge, MA: M.I.T. Press, 1968.

Robins, C., & Shepard, R. N. Spatio-temporal probing of apparent rotational movement. Perception & Psychophysics, 1977, 22, 12-18.

Rosch, E., & Mervis, C. Family resemblances: Studies in the internal structure of categories. Cognitive Psychology, 1975, 7, 573-605.

Rumelhart, D. E., & Levin, J. A. A language comprehension system. In D. A. Norman & D. E. Rumelhart (Eds.), Exploration in cognition. San Francisco: W. H. Freeman, 1975.

Shepard, R. N., & Judd, S. A. Perceptual illusion of rotation of three-dimensional objects. Science, 1978, 191, 952-954.

Shepard, R. N., & Metzler, J. Mental rotation of three-dimensional objects. Science, 1971, 171, 701-703.

Shepard, R. N., & Podgorny, P. Cognitive processes that resemble perceptual processes. In W. K. Estes (Ed.), Handbook of learning and cognitive processes (Vol. 5). Hillsdale, NJ: Erlbaum, 1978.

Zadah, L. Fuzzy sets. Information and Control, 1965, 8, 338-353.

Appendix 1
Implementation of Relationships

The processing mechanism for Relationships is embedded within the Proteus activation framework, described in detail in Levin (1976). Concepts are stored in an interconnected semantic network long term memory. Some processes are "boundary concepts", defined in part by connection to activity outside the scope of what is being modeled. Some of these are output boundary concepts, such that their activity causes action outside the scope of the current model. Others are input boundary concepts, and thus can be activated by events outside the scope of the model.

Processing in a particular task may start when some of these input boundary concepts are activated. When a concept is activated, an entity called an "activation" is created in a dynamic temporary store called the "workspace". Each such activation has associated with it a real numbered salience value. In the actual implementation, there are actually two real numbers, the "current salience" and the "new salience". To simulate concurrent processing, the implementation cycles through all the activations, processing each a little bit. The impact of each activation on others depends on its current salience, but modifies the other activations' new salience values. Thus the order of processing through each cycle has no impact on the outcome, and processing is equivalent to concurrent processing outside the time grain of one cycle. Each activation also has a pointer to its concept in long term memory, and links to other activations in the workspace that it influences.

A relationship is defined as a concept in long term memory, and operates through an activation of that concept. It is linked to activations for its parameters (themselves concepts with activations), and operates to modify them in a way determined by its long term memory representation. This representation specifies an "ideal" relation among the parameters. An activation operates to instantiate this relative knowledge by modifying the particular values in the workspace.

A relationship determines the "ideal" value for a parameter, given the current values of all the other parameters and the relation defined in long term memory. It then "pushes" this ideal value, by activating that value with a strength proportional to the current salience of the relationship. Thus a highly salient relationship changes the values of its parameters more than less salient ones.

Similarly, the salience of the relationship itself is dependent on the degree of match between the ideal and actual values of each of its parameters. If there is a large degree of mismatch, then the relationship becomes less salient. In this way, the salience of the relationship captures to some extent the degree to which the relationship holds.