Low pass filter - ideally attenuates high frequency modulations while allowing low frequency modulations to pass unchanged
High pass filter - ideally attenuates low frequency modulations while allowing high frequency modulations to pass unchanged
Band pass filter- passes a band of frequencies (and attenuates others)
Notch filter- removes a (usually small) range of frequencies (often around 60Hz)
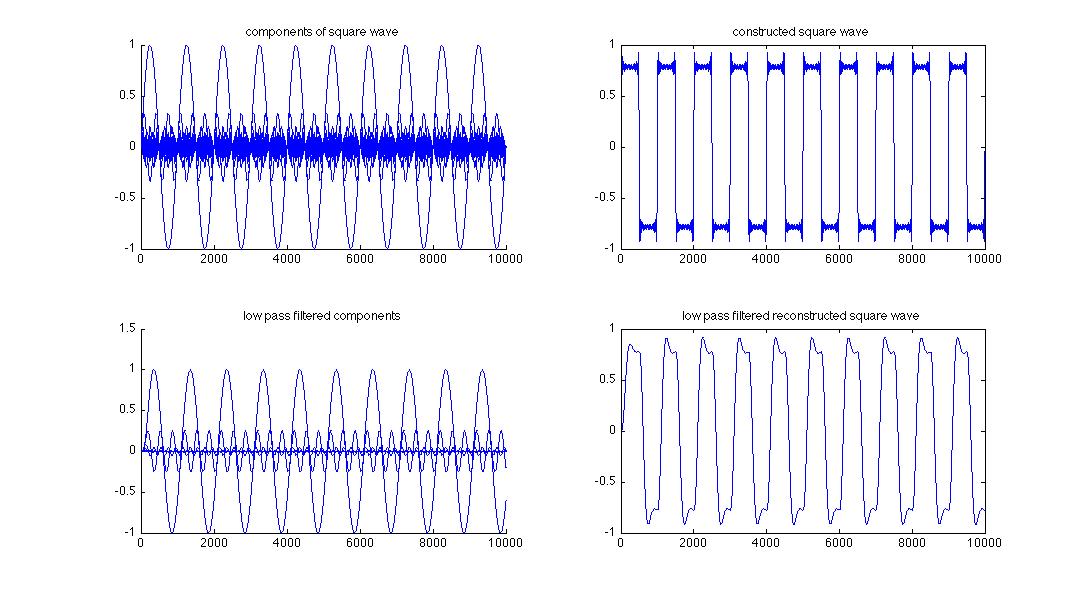
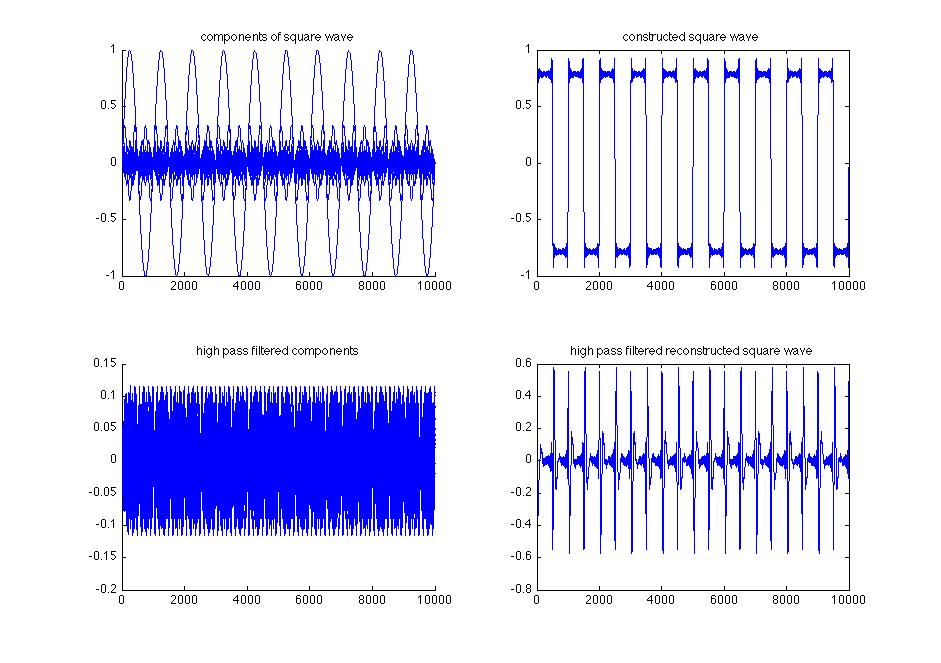

external link to animated synthesis of a square wave from sinusoids (from wikipedia)
link
If the noise has zero mean then one way to low pass filter is to average over nearby signals
Causal filter - only uses values that have already occured. In other words x(t) can not be affected by x(t+b) for any positive b. Here is a causal LPF (low pass filter)
x(t) is the raw signal at time t
xlp(t) is the low-passed signal at time t
xlp(t) = a*x(t) +(1-a)*x(t-1) (here a is a number between 0 and 1)
Here is a non-causal LPF
xlp(t)= a*x(t)+(1-a)/2*x(t-1)+(1-a)/2*x(t+1) (again a is a number between 0 and 1)
A recursive filter is a filter that uses one or more of its outputs as an input. Here is a recursive causal LPF.
xlp(t)=a*x(t)+(1-a)*xlp(t-1)
recursive filters are also called IIR filters (infinite impulse response)
non-recursive filters are called FIR filters (finite impulse response)
One can get a high pass filter by subtracting low-passed signal from the signal. This makes sense because a high pass filtered signal maintains only the high frequencies so we take the original signal and remove the low pass filtered signal (that maintains only the low frequencies) and we are left with the high frequencies.
xhp(t) = x(t) - xlp(t)
Here are some pdf slides on practical issues in filtering EEG signals offline slides online slides
Sampling
The voltage signal that EEG is recording is a continuous signal, but to process it in the computer it is sampled at discrete times. This is done at a specific sampling rate that specifies the number of samples per second. To avoid aliasing, you must sample at least twice as fast as the highest frequency in your signal (Nyquist Theorem) . (This is done in the hardware, so the hardware will perform a low-pass filtering before sampling, however if you downsample further, you may need to further low-pass the signal).
Want to filter out frequencies higher than your Nyquist frequency (half sampling rate) in order to prevent aliasing. Aliasing refers to the distortion that can happen to a reconstucted sampled signal. It results because different signals (e.g. different frequency sinusoids) may have identical sampled values. Most algorithms (including your brain) will then assume that the lowest of the possible frequencies was the original signal.
More info on aliasing wikipedia aliasing This figure is from that page
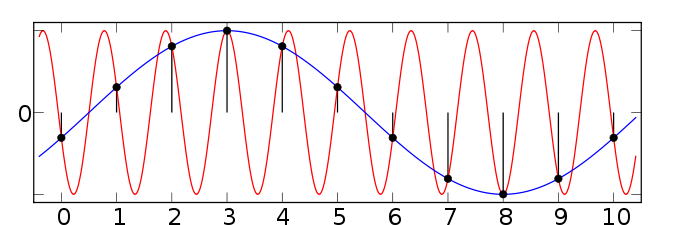
aliasing demos demo 1 demo 2 demo 2newlink
aliasing videos video1 (sound demo) video