%% DATA now available to you as hw3bdata.mat
load hw3bdata.mat
% look at the first face
viewcolumn(faces(:,1))

% compute the mean face (note this computes the rowwise mean)
meanface=mean(faces,2);
% subtract the mean face from all faces. Do help repmat to understand
% this command. repmat creates one matrix with multiple copies of the
% first argument (meanface). The multiple copies are tiled with 2nd
% argument (1) vertically and 3rd aRgument (48) horizontally. Try this
% with a small matrix and different 2nd and 3rd arguments to get a feel
% for it.
%% e.g. try repmat(4, 5, 2)
%% repmat([4 1], 5, 2)
%% repmat([4 1]', 5,2)
facesz=faces-repmat(meanface,1,48);
% Look at the mean face
viewcolumn(meanface);

%%% Using the trick discussed in class, we first find the eigenvectors
%%% of Z'Z
[Vp, Dp]=eig(facesz'*facesz);
%%% sort them in order of decreasing eigenvalues
[V,D]=eigsort(Vp,Dp);
%%% This is the second part of the trick -- make sure you understand why
%%% this is necessary. clicker1 link
U=facesz*V;
%%% We want normalized (length 1) eigenvectors
normU=normc(U);
%%% Look at the eigenfaces (Principal Component directions) (e.g. look at
%the first one)
viewcolumn(normU(:,1));
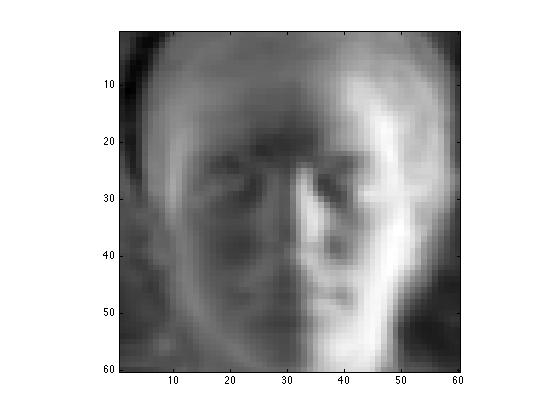
%%% Look at moving away from the meanface in the direction of the 1st
%principal component direction
viewcolumn(meanface+normU(:,1))
%%%% construct a movie of passing along the direction of the first
%%%% principal component (shows you what the direction of greatest
%%%% variance in the data is
for i=-20:.5:20
viewcolumn(meanface+i*normU(:,1));
M(2*i+41)=getframe;
end
%%% Play the movie
%%%%%% This movie shows what it would look like to fly through your
%dataspace along the first principal component direction
movie(M) %%% click on movie below to make it "move"
%%% Modify testface to view different faces
testface=1
viewcolumn(faces(:,testface))
%%% compute principal components for testface
c=normU'*(faces(:,testface)-meanface);
numcomponents=47 %% (This is the minimum of the size of the space, and
%% the number of patterns -1). Be sure you understand
%% why this is the case (Hint: what is the
%% dimensionality of the space defined by two points in
%% 3D space? )
%%% done the fast way (reconstruct with all pcs
facereconstructed = meanface + normU(:,1:47)*c(1:47)
viewcolumn(facereconstructed);
%%% note this is done the slow way to watch as you add in each principal
%component
facereconstructed =meanface; %% (0th order reconstruction is to
%represent every face with the mean face
for i=1:numcomponents
facereconstructed = facereconstructed + normU(:,i)*c(i);
%% for fun watch it as you reconstruct
viewcolumn(facereconstructed);
title(sprintf('reconstructed with %d eigenfaces',i));
text(55,55,sprintf('%d',i),'FontSize',20);
%% and for more fun, create a movie
MM(i)=getframe;
end
%%% look at the final result in a new figure
figure
viewcolumn(facereconstructed);
%% This movie shows the reconstruction of face 1 with varying numbers
%% of principal components
movie(MM);


