ALLOMETRY

This handout describes the application of allometric analyses to some primate problems. The approach is extremely powerful and is central to understanding comparative studies; at first it may seem overwhelming but a few examples should help straighten it out. Because of the [possible] tie-in between brain size, complex primate behavior, and human evolution, the examples all come from analyses of relative brain size--but the basic approach can be applied to any comparison of a morphological feature across individuals/populations/species etc.

Most biological functions increase as some power of body size. For example, more energy is needed to "run" an elephant than to run a mouse; as body size increases, so does the energy needed by the organism. More cognitively, if bodies are operated by brains, then it seems reasonable that the larger the body, the larger the brain needed to operate it--more nerves needed to coordinate more muscles, etc. However, such size-based relationships are rarely 1:1 (that is, it is rare to have a 1-unit increase in body size produce exactly a 1-unit increase in metabolic rate, or brain size, or whatever).

So, we are interested in the relationship between body size and brain size; we expect larger animals to have larger brains, but we want to know more about the relationship for TWO REASONS:

First, knowing something about the general relationship might tell us something interesting about brains and cognition and intelligence in general.
Second, if there is a general relationship, then we want to factor it out when talking about brain size in relation to cognition: cows have bigger brains than most monkeys, but that probably has more to do with having really bigger bodies than with unsuspected cow intelligence.

For starters, it makes sense to go out & measure a bunch of primates' body and brain sizes:
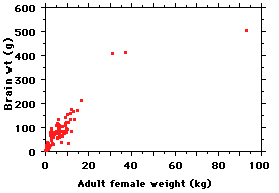Here is a plot of the data for 117 species; adult females were used because it simplifies how one deals with sexual dimorphism, and for various theoretical reasons female mammals are thought to be the "ecological sex", with males more a derived form of females (driven by sexual selection). Here is what the data look like; note that body weight is given in kilos (1,000 gm) - so multiply the body weights by 1,000 to get them into the same units as brain weights.

Sure enough, bigger-bodied species tend to have bigger brains (wow). But how do we express that relationship?

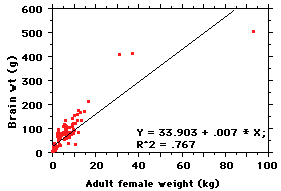Well, why not do a regression of brain size on body size? There are several methods for calculating a regression (see below), but the principle is simple: it is a line of best fit between the variables. And the line itself can be described by a simple equation of the form

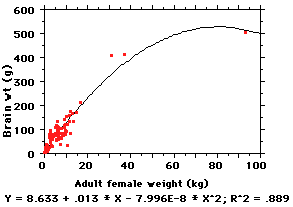
Try a nonlinear regression, of course. Here is a "2nd-order" regression (note the new x² term in the equation) and you can see that now the line explains about 89% of the variation -- which is pretty good.

HOWEVER, 2nd-order equations are cumbersome and difficult to compare (say we wanted to know if the relationship between body size and brain size was the same in primates and cetaceans [Y = -6.162 + 2.834 * X - .202 * X²; R² = .922 for a sample of 21 whales and dolphins] -- now what? Two horrendous equations...). Also, most of the 114 non-ape species are still packed into the dense cloud of points at the left; basically, most primates weigh between 1,000- 15,000 gms (1-15 Kg) and one can't get a visual feel for variation amongst them. It is hard to do much with such a figure and equation.

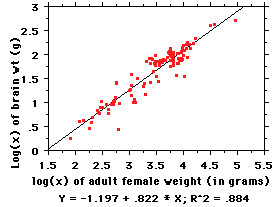So we convert the raw data to base-10 logs, as in the figure at left (note units need to be the same, so body weight is now in grams). As you can see, when the data are expressed as logs, they fit a nice easy linear equation, the points are spread out so we can see what is going on, and the R² value is essentially unchanged (the slight difference between 0.889 in the untransformed data and the 0.884 here is due to the transformation; don't worry about it, it is small).

Now: the equation for the line here is of the familiar "y=mx + b" form, but the "y" and "x" here are actually log(brain weight) and log(body weight)

This is an allometric equation;"allo" comes from Greek allos = "other", in this case "other than metric" -- that is, nonlinear (the alternative is a linear or isometric equation, a 1:1 relationship -- e.g., for every kilo of body weight, add 20gm of brain). We merely made it linear by the log transformation in order to visualize it better and to be able to work with it more easily.

To express the same nonlinear relationship directly -- that is, with an equation in which x is body weight, not log(body weight)-- we convert from the above which is really

to the standard form for allometric equations, y = bx^m

EXAMPLE: how large do we expect the brain of a 1,000 gram (1kg) female monkey to be, based on the above regression?

1) in y=mx + b form (as shown in the graph above), y = -1.197 + 0.822
This is the empirically derived equation for the regression of brain size on body size in the sample above, and so is our best tool for this prediction.

(...well, what is the log of 1,000?)

Log(1,000) = 3 (recall: 1,000 = 10³) so log(y) = -1.197 + 0.822 * 3

= 1.269

y = 10^1.269 = 18.6 gm

2) or using y = bx^m, after converting "b" from log: 10^-1.197 = 0.064:

y = 0.064 * 1,000^0.822
= 18.7 g

(18.6 and 18.7 are within rounding error). So that's how we can convert between the two forms of the equation (with one minor but annoying caveat: we all learned the equation for a line as y=mx + b, where b = intercept and m = slope. I kept the m=slope in the above so you could see the relationship between the two forms of the equation, but for some reason having to do with perversity of mathematicians, the allometric equation's general form is usually written as y=bx^a where b is called the "allometric coefficient" and the slope is designated by an a, not m. Oh well, could be worse.

One last bit of mathematical fun before getting back to (more or less) biology: there are actually several different ways to compute the line of best fit. Researchers get into endless arcane arguments about which method is better for which sort of analysis; the preferred methods seem to be major axis or reduced major axis analysis.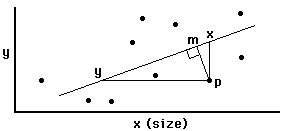

Regression: minimizes line X-P
Major axis (=principle components) analysis: minimizes line M-P
Reduced major axis analysis: minimizes area of triangle Y-X-P

TO RECAP:
The general form of the allometric equation is y = bx^a where y = measure/process in question, x is size (usually weight), a is the allometric exponent (which tells you the relationship between x & y), and b = a constant (the allometric coefficient). For example, among mammals the basal metabolic rate (BMR, measured in Kcal/hour) = 3.8(weight)^0.75

The Important Thing To Realize is that in this equation (and other allometric equations), the 3.8 and the 0.75 are empirically derived. You weigh a whole lot of animals, measure their BMRs, graph the results on a log-log plot, and discover that the regression line has slope 0.75 and intercepts the y-axis at 3.8. Obviously, it makes a difference which species you look at. Different taxa have different values for b, and the value of the exponent can depend on what you're studying (BMR, here). This means that you can find different values reported for, say, the slope of the line relating brain size to body size--it depends on the sample.

AAARRRGHHH! Why do we CARE? I mean, we go through all this math, and at the end discover it is a lot of work that yields a precise answer, but different answer depending on the sample used; what is the point? What does the slope TELL us that we didn't already know???

It so happens that basal metabolic rate (BMR) increases as a ca. 0.75 power of weight--a baboon needs absolutely more energy than a marmoset, but a good bit less per gram (why it is 0.75, who knows-- it is an empirical finding). On the other hand, for purely geometric reasons, the surface area of same-shape solids increases as a 0.67 power of volume (which is about the same as weight, as long as we stick with animals). If relative brain size is related to body surface area (logical enough; our skin is a neurological interface, after all), then brain size should scale to ca. 0.67 power of body weight; if BMR is the critical factor* then the power function should be close to 0.75. Hence the interest in working out the slope--it can tell us what is biologically important.

* Reasonable; high metabolism, more energy needed to fuel the system, and more energy available for doing complex things -- like look for the source of that energy!

Now let's get into application of the method to the problem of intelligence and brains:

1) What might the slope tell us?

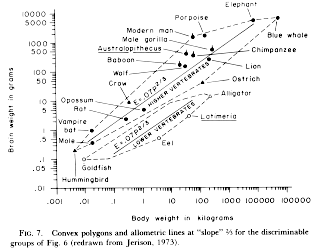One of the first and most widely cited allometric analyses is Jerison's work on relative brain size in vertebrates. In the figure at left (from Jerison 1983), you can trace the two lines backward to see that they in fact intercept the Y-axis at 0.07 and 0.007, as SHOULD be indicated by the allometric coefficients in the equations (the lower 0.07 is a typo that does not appear in the original 1973 paper; it pays to read critically!). The ten-fold difference in intercept supposedly reflects a difference in grade; the "lower" vertebrates doing something fundamentally different from the "higher" vertebrates in terms of brain/body allocation. However, the slopes shown are equal (allometric exponent = 2/3, or 0.667), indicating that within each grade, the same set of rules apply to how the brain is scaled with respect to body size. Since 0.67 is the exponent for surface area:volume relationships in solids, and there is a plausible argument for surface area being functionally related to the nervous system's basic requirements, this suggests that relative brain size in vertebrates is "driven" by body surface area (rather than being, say, a simple isometric relationship), with "higher" vertebrates applying the same relationship but "scaled up" to reflect overall greater emphasis on intelligence.

Cool, except Jerison cheated. Well, fudged. As he explains in his papers (the figure here is from 1983), the lines shown are actually not regression (or major axis or whatever) lines at all; they are lines of slope 0.67 that he fitted by eye to the data points, because he thought surface area was the key and the lines look pretty close. This is not the way to do science (in his defense, he was the first to really even think of this sort of problem, and pioneered the field; pioneers often get the big picture right but goof on the details; besides, he did use quotes around the word "slope" in the caption). Most subsequent analyses of large numbers of mammals have found slopes much closer to 0.75, favoring an underlying BMR basis to brain size; however there are these interesting deviations (remember, for 117 primates we got 0.882, and for the smaller cetacean sample, slope is 0.376 [but restrict it to dolphins, and it's 0.682; for 139 primates and cetaceans combined, the slope is... 0.673!]). There are many papers and several books written just on the subject of allometry; let's leave it that the meanings of slopes in brain:body analyses are still being investigated. In general,

1) for large samples the slope tends toward 0.75 suggesting something metabolic is involved;
and

2) as one narrows the taxonomic unit of analysis (from mammals to Family to Species, say) the slope tends to decrease, to the point that within species the brain:body slope is close to 0 -- body size explains very little of the variation observed in brain size within species.

The overall relationship between body size and brain size, as reflected by the slope (allometric coefficient), might tell us something about the fundamental nature of determinants of brain size in broad taxonomic groups. However, we are also interested in species (or genera, etc): e.g., are gorillas large-brained for their size? Underlying this is obviously the question, "are they 'smart'?"; there are lots of problems using brain size as an indicator of intelligence and here we are addressing only how the method works, not whether it should be used). Underlying this is the intuition that absolute brain size is not a good indicator of intelligence; if it were, blue whales would be the smartest animals on earth--something for which there is zero behavioral evidence. Rather, we'd like to "factor out" that portion of brain size that is "due to" body size, leaving behind relative brain size.

Clearly, since the line of best fit (regression, major axis, or reduced major axis) is calculated based on the data, it should be possible to calculate exactly how far each point is from the line; it is, and these numbers are called residuals. One can then use these residuals in one way or another to calculate an index of brain size relative to what is predicted for an animal of that body size. Different researchers use different indices (two you might run into are "comparative brain size" or CBS, and "encephalization quotient" or EQ). Animals with large EQs are thought to be relatively "smart" and those with small EQs are... not (for example, the siamang in the figure below). CAUTION: There are 3 possible lines of best fit, and since this is empirical of course the exact line--and hence residuals--will depend on which species are in the sample, AND there are different ways to calculate the EQ (should you base the human EQ on all mammals, on just "primitive" mammals (compare to a baseline), or on just primates?). Hence values of EQ or CBS in the literature range widely; I've seen between about 4 - 8 for humans (one of, if not the most, encephalized animals). Just be careful when comparing results across studies, and read the methods carefully!

1) The data points themselves.

A species doesn't have a body, or a brain. How many specimens were measured? Zoo animals (often obese)? Sexual dimorphism? Geographical or racial variability? No easy answers. Read the methods sections of papers!

2) The "part/whole" problem.

Properly speaking, we are wrong to correlate brain weight with total body weight, because total body weight includes brain weight and so artificially strengthens the correlation between the "two" variables. Primate brains aren't usually such a large proportion of the body weight that this bias is important, but if you were interested in e.g., muscle mass, clearly you'd want to compare muscle mass not with body weight, but with the weight of everything left with muscle removed (messy research, that). And it may turn out to be an important problem for brain allometry...

3) "Galton's problem."

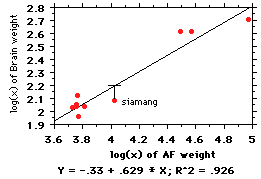Galton was one of the first to use regressions in biology, and he had a problem that we still have: independence of the points. It's best illustrated with an example: Let's say we are interested in brain:body relationships among the apes; the log:log regression is shown at right. Note there are 6 species of gibbon, 1 siamang, and chimps, orangs, and gorillas. The regression line fitting these points is y= (-.33) + .629(x) (note that the coefficient, 0.629, is less than the 0.822 found above for primates-- illustrating the point about lower slopes as one gets narrower taxonomically). But when you think about it, those 6 species of gibbon are just local varieties of the same animal, eating the same things, with the same social organization, etc. Those 6 points are not independent of each other; it is just sort of a biogeographic historical accident that there are so many species (maybe... ).

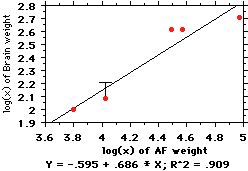This figure shows what happens when you average the 6 gibbons together. The change isn't big, but it's there (note the "T" bar on the point representing siamangs, illustrating how the distance between the point and line has shifted--in effect, siamangs have gotten "less small- brained" because we pooled the gibbons). The problem is deciding which species are "independent." EG guenons: many species, many just allopatric versions of each other; BUT there are sympatric ones that clearly are "different" in what may be important ways (cf. multimale, semiterrestrial vervets and unimale, arboreal redtails at Kibale). If it was just allopatry & sympatry, no problems; but what about sympatric Kibale redtails and blue monkeys (which sometimes interbreed)? Harvey et al. (1987) discuss the problem (& their solution) in the top right column of p. 182.

4) Interpretation--What does it MEAN?

Harvey et al. conclude that the brain-body slope is based on BMR because "When the analysis is repeated with Homo removed, the exponent is reduced such that 0.75 lies within its 95% confidence limits (see Table 16-3)" (p. 187); valid conclusion, but those confidence limits are 0.74 - 0.99 -- 0.75 sure isn't FAR within that range. Their method is better than Jerison's (fitting a line by eye to reflect the theory he liked) but it isn't clear that the issue is solved (attention has been turning to the relationship between mother's BMR and relative brain size of newborns).

Or: if you code primates by diet as folivores (primarily leaf eaters) or frugivores (primarily fruit eaters) and then regress brain on body size, the folivore species tend to fall below the line--that is, they tend to have lower EQs than frugivores. The relatively small brains of folivores have been used to argue that ecological pressures have been important in the evolution of intelligence. BUT: that assumes relative brain size is a measure of intelligence (comparing DIFFERENT SPECIES, it seems to hold). And it assumes nothing else is "going on"; several problems with that assumption have been pointed out: (a) folivores may have lower BMRs, and this may be responsible for their brain size, not any lack of need for intelligence; (b) folivores have big guts, normally full of fermenting leaves; weight may be misleading by "artificially" increasing body size and hence lowering relative brain size. Could try length, but that is sensitive to body build. How can we compare fat folivores with skinny frugivores?

---

A sampler of references in case you want to pursue this (hey, someone might):

1. Deacon, T. W. (1988). Human brain evolution: II. Embryology and brain allometry. pp. 383-415 IN Jerison, H. J. & Jerison, I. (Ed.), Intelligence and Evolutionary Biology. Berlin: Springer-Verlag.

2. Deacon, T. W. (1990). Fallacies of progression in theories of brain-size evolution. Int. J. Primatol. 11: 193-236.

3. Gould, S. J. (1975). Allometry in primates with emphasis on scaling and the evolution of the brain. Contr. Primatol. 5: 244-292.

4. Harvey, P. H. (1990). Life-history variation: size and mortality patterns. pp. 81-88 IN DeRousseau, C. J. (Ed.), Primate Life History and Evolution. New York: Wiley-Liss.

5. Harvey, P. H., Martin, R. D. & Clutton-Brock, T. H. (1987). Life histories in comparative perspective. pp. 181-196 IN Smuts, B. B., Cheney, D. L., Seyfarth, R. M., Struhsaker, T. T. & Wrangham, R. W. (Ed.), Primate Societies. Chicago: University of Chicago Press.

6. Harvey, P. H. & Pagel, M. D. (1991). The Comparative Method in Evolutionary Biology. Oxford: Oxford University Press.

7. Holloway, R. (1979). Brain size, allometry, and reorganization: Toward a synthesis. pp. 59-88 IN Hahn, M. E. & al, e. (Ed.), Development and Evolution of Brain Size. New York: Academic Press.

8. Jerison, H. F. (1983). The evolution of the mammalian brain as an information-processing system. pp. 113-146 IN Eisenberg, J. F. & Kleiman, D. G. (Ed.), Advances in the Study of Mammalian Behavior (Spec. Publ. Amer. Soc. Mamm. 7). Pittsburgh: American Society of Mammalogists.

9. Jerison, H. J. (1979). The evolution of diversity in brain size. pp. 29-57 IN Hahn, M. E. & al, e. (Ed.), Development and Evolution of Brain Size. New York: Academic Press.

10. Leroi, A. M., Rose, M. R. & Lauder, G. V. (1994). What does the comparative method reveal about adaptation? Am. Nat. 143: 381-402.

11. Martin, R. D. & Harvey, P. H. (1985). Brain size allometry: ontogeny and phylogeny. pp. 147-173 IN Jungers, W. L. (Ed.), Size and Scaling in Primate Biology. New York: Plenum.

12. Martin, R. D. & MacLarnon, A. M. (1990). Reproductive patterns in primates and other mammals: the dichotomy between altricial and precocial offspring. pp. 47-79 IN DeRousseau, C. J. (Ed.), Primate Life History and Evolution. New York: Wiley-Liss.

13. Ross, C. (1992). Basal metabolic rate, body weight and diet in primates: an evaluation of the evidence. Folia primatol. 58: 7-23.

14. Sawaguchi, T. (1992). The size of the neocortex in relation to ecology and social structure in monkeys and apes. Folia primatol. 58: 131- 145.

15. Smith, R. J. (1993). Logarithmic transformation bias in allometry. Am. J. Phys. Anthropol. 90: 215-228.

    Back to course handout menu

    Back to Moore's home page

    Jump to overview of BioAnthro at UCSD & elsewhere

    
    Uploaded: 1 Oct 1999
    revised 5 Oct 2000 -- thanks to Graham Horgan for feedback!