![]()
Where
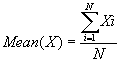
In words:
Z-scores
What they are:
--- They are standardized scores. They give you the location of a score in a distribution of scores in relation to the mean in standard deviation units.
--- The mean of a set of Z-scores is always 0.
--- The standard deviation (and variance) of a set of Z-scores is always 1.
Example:
Zxi=+1 is a score of variable X that is one standard deviation above the mean
Zxi=-1.5 is a score of variable X that is one and a half standard deviation below the mean
Formula:
![]()
Where
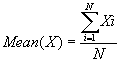
In words:
You add up all the scores and divide by the number of scores you have added.
And where:
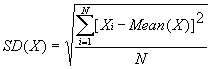



 In words:
In words:
You calculate the difference between each value and the mean. Then you square these differences one by one. Then you add all up. Then you divide by the number of squared differences you have added. (This is the mean squared difference from the mean or variance.) Finally, you take the square root to get the standard deviation.
ANOTHER EXAMPLE.
Take five children of ages from 2 to 10 as follows. (X is now Age and XI is the Age of the ith child. Adam, the 1st child is 2 years old.) Calculate the Z-score for each.*
|
CHILD |
i |
Xi |
Xi-Mean(X) |
Zxi |
|
Adam |
1 |
2 |
2-6=-4 |
-4/2.83= -1.41
|
|
Erica |
2 |
8 |
8-6=+2 |
+2/2.83= +0.71
|
|
Olivia |
3 |
6 |
6-6= 0 |
0/2.83= 0
|
|
Dylan |
4 |
4 |
4-6=-2 |
-2/2.83= -0.71
|
|
Lisa |
5 |
10 |
10-6=+4 |
+4/2.83= +1.41 |
Mean(X)=6
SD(X)= 2.83
* Numbers are rounded.